Learning Linearity in Audio Autoencoders

📄 Paper (arXiv) GitHub

Autoencoders are powerful tools for learning compressed representations of sound, but their internal "latent" spaces are typically complex and non-linear. While in some applications this might be by design to capture high-level representations, it is often desirable to have low-level control over audio manipulations directly in the latent space. For example, adding the representations of two sounds doesn't create the representation of their mixture.

We introduce Linear Consistency Autoencoders (Lin-CAE), a simple training method that induces linearity in the latent space of a high-compression consistency autoencoder. This is done through data augmentation, without changing the model's architecture or loss function. While we apply this method to consistency models, a type of autoencoder where the decoder is a generative diffusion model, the approach is general and can be applied to any autoencoder architecture.

Linear autoencoder properties
A linear decoder respects latent space scaling (homogeneity) and addition (additivity). Linear operations in the latent space correspond to linear operations in the audio domain.

Properties of a linear autoencoder

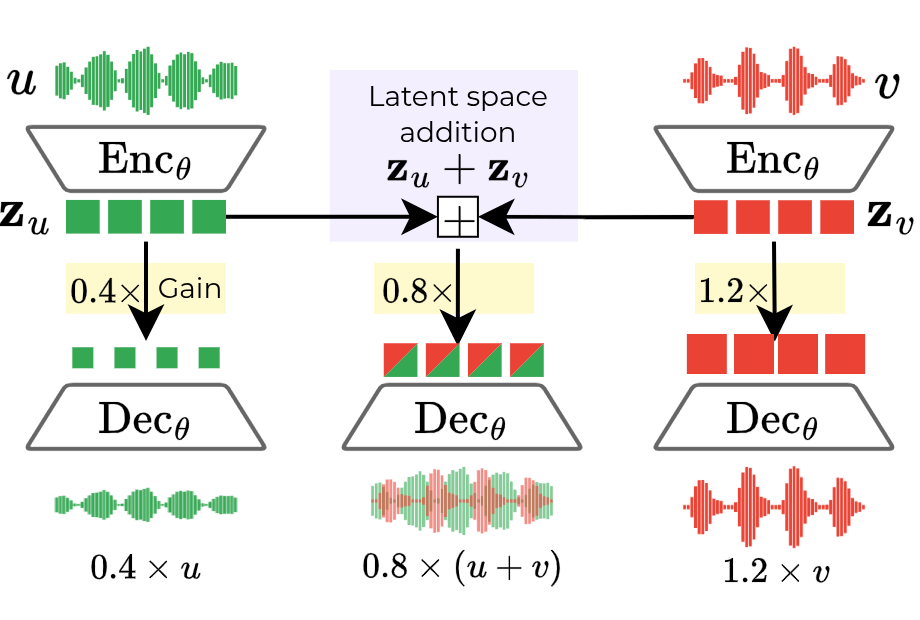
A linear latent space allows for intuitive and efficient audio manipulation directly in the compressed representation. Let's denote the encoder as \(\operatorname{Enc}(\cdot)\) and the decoder as \(\operatorname{Dec}(\cdot)\), and a latent tensor as \(\mathbf{z}_x = \operatorname{Enc}(x)\) for an audio signal \(x\).

  • Homogeneity (Scaling): You can control the volume of a sound by simply multiplying its latent tensor by a scalar.
    \(\operatorname{Dec}(\textcolor{magenta}{a} \cdot \mathbf{z}_x) \approx \textcolor{magenta}{a} \cdot \operatorname{Dec}(\mathbf{z}_x)\)
  • Additivity (Mixing): You can mix multiple sounds by adding their latents together.
    \(\operatorname{Dec}(\mathbf{z}_u + \mathbf{z}_v) \approx \operatorname{Dec}(\mathbf{z}_u) + \operatorname{Dec}(\mathbf{z}_v)\)

Combining these properties unlocks some applications such as source separation via subtraction. By subtracting the latent of an accompaniment from the latent of a full mix, we can isolate any stem. For vocals, this can be expressed as: \(\operatorname{Dec}(\mathbf{z}_{\text{mix}} - \mathbf{z}_{\text{accomp}}) \approx \operatorname{Dec}(\mathbf{z}_{\text{vocals}})\)

Audio Demos

The interactive players below compare our model (Lin-CAE) against a few baseline autoencoders on test samples from the MUSDB18-HQ dataset.

We recommend using headphones. Each row in the player performs a different operation in the latent space.

  • Autoencoded Mix: The baseline reconstruction of the full mix.
  • Latent Addition: We add the latent vectors of four stems (vocals, drums, bass, other) and decode the result.
  • Original Vocals: The ground truth vocal stem, for reference.
  • Separated Vocals: We subtract the latent vector of the accompaniment (drums, bass, other) from the latent vector of the full mix and decode the result.
  • Latent Scaling: We multiply the vocal latent vector by a scalar and decode the result.

The following controls are available:

  • Stop All: Stop all currently playing audio.
  • Sync Playback: When enabled, switching between models or stems will sync the playback position across all audio elements. When disabled, each audio element will play from the beginning.
  • Loop: When enabled, the audio will loop continuously.

Warning: Please turn your volume down before playing. The baseline models (M2L, Stable Audio VAE) can produce loud, unpleasant, and intense sounds when attempting linear operations they were not trained for.

Citation

If you use our work in your research, please cite our paper:

@misc{torres2025learninglinearityaudioconsistency,
      title={Learning Linearity in Audio Consistency Autoencoders via Implicit Regularization},
      author={Bernardo Torres and Manuel Moussallam and Gabriel Meseguer-Brocal},
      year={2025},
      eprint={2510.23530},
      archivePrefix={arXiv},
      primaryClass={cs.SD},
      url={https://arxiv.org/abs/2510.23530},
}